赛题内容是,模拟一个270°的扇形在直线上滚动的情景,并画出扇形“圆心”的轨迹。
模拟滚动的情景,可以有两种方法,但是要绘制轨迹,就不得不减少一种方法。网络画板构造轨迹,必须有主动点和目标元素两个几何图形。
这里不说具体步骤,只谈一下我的想法。

方法/步骤
-
1
先来剖析一下这个滚动过程:
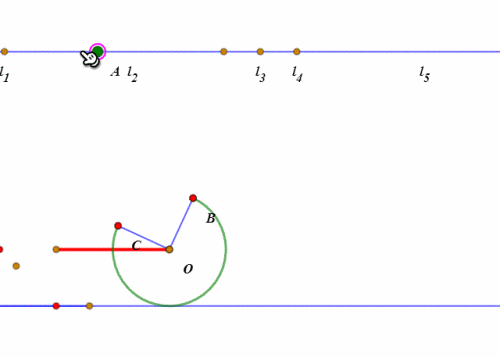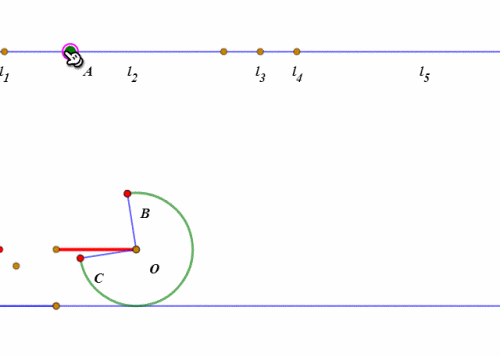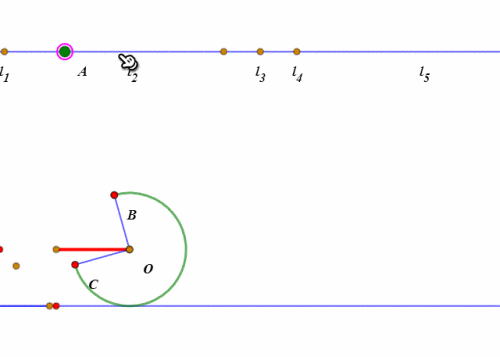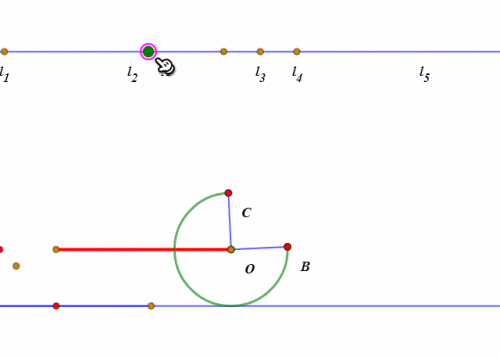
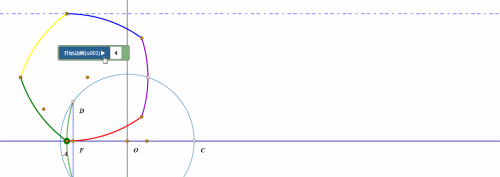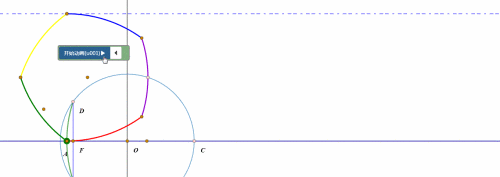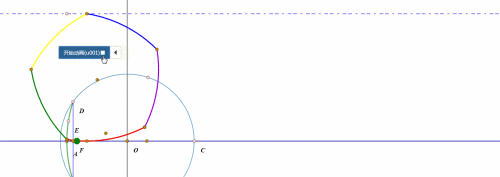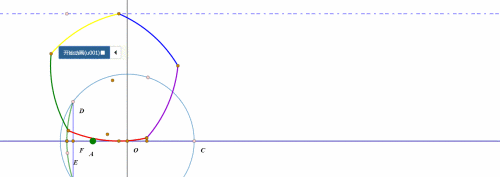
当扇形开口朝下、BC处于水平状态的时候,所谓的“滚动”,其实就是整个扇形绕点C旋转45°。
然后就是扇形的圆弧贴着直线滚动了。
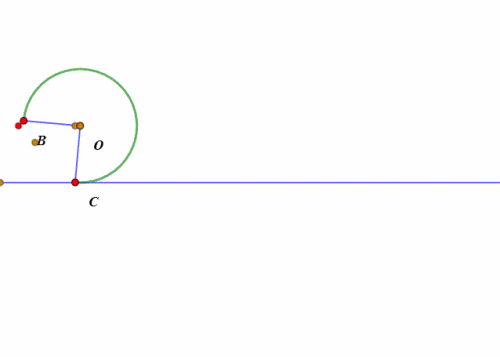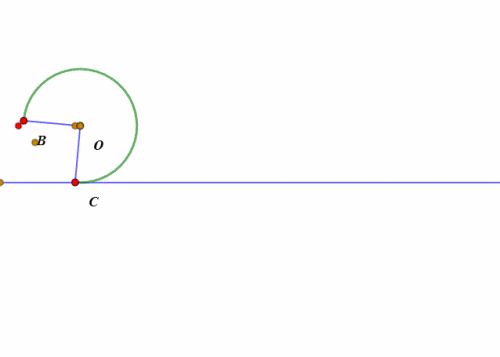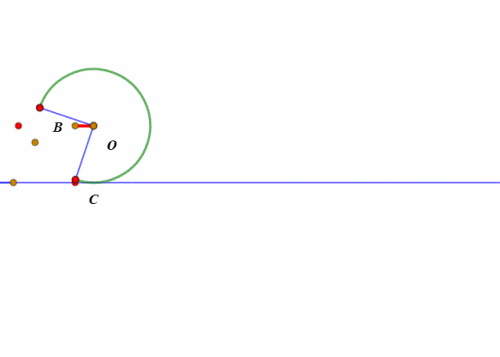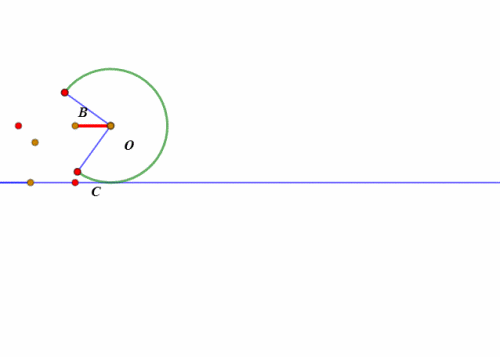
-
2
圆弧的滚动,和圆的滚动的实现方法大同小异,都是“绕圆心旋转”和“圆心平移”。
当“旋转”的弧长等于“平移”的距离,那么这就是“纯滚动”。
-
3
可以说,圆在直线上的滚动,就是旋转+平移。
那么,其它图形在直线上的滚动会是怎样的呢?
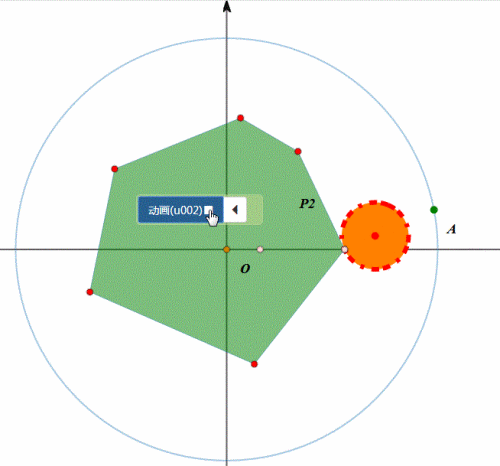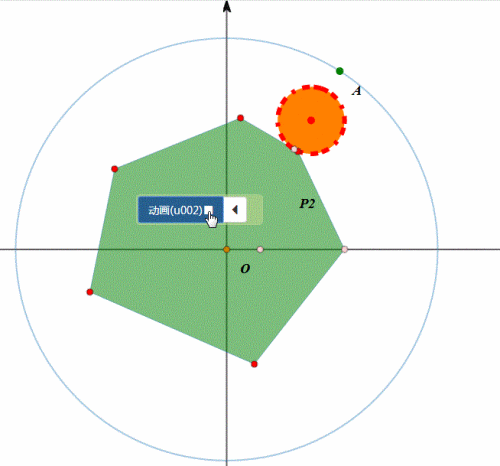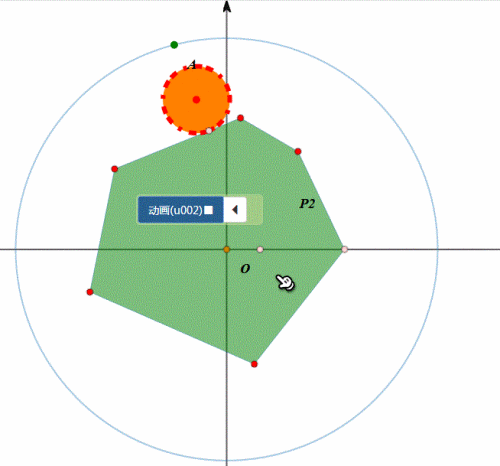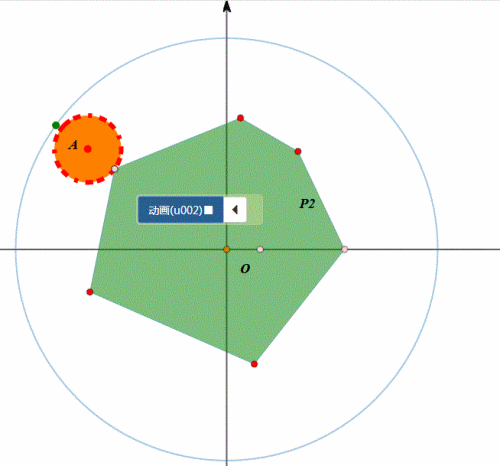
下图是任意四边形在圆上的滚动,其实就是依次绕着各顶点旋转。
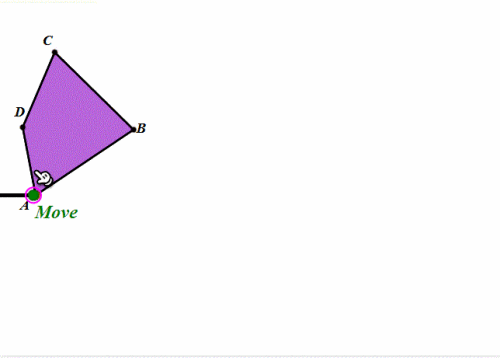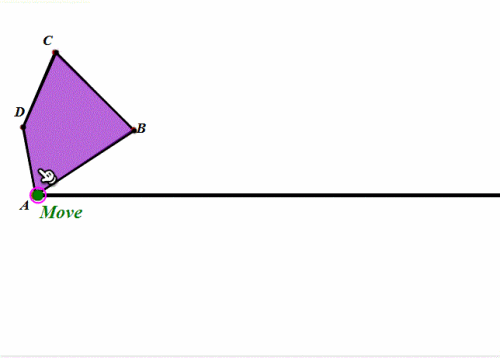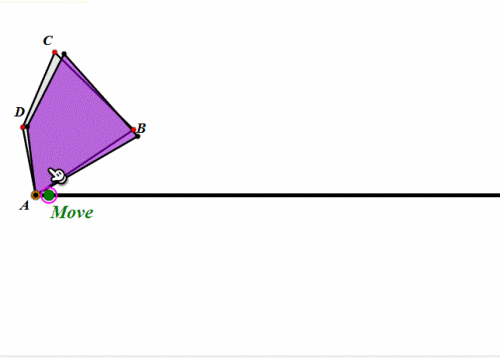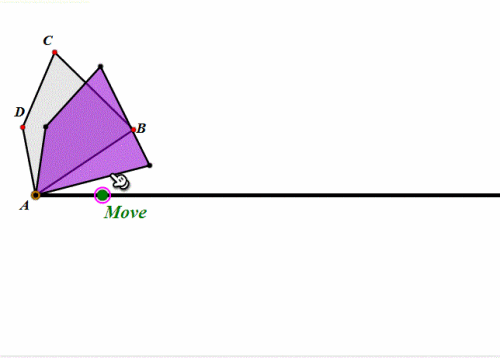
-
4
等宽曲线在直线上的滚动,可以分解为若干个扇形的滚动。这个多说无益,大家应该看课件,自己思考。
至于更一般的情形,如:椭圆在直线上的滚动,三叶玫瑰线在直线上的滚动,等等,目前还没有网络画板的课件。

-
5
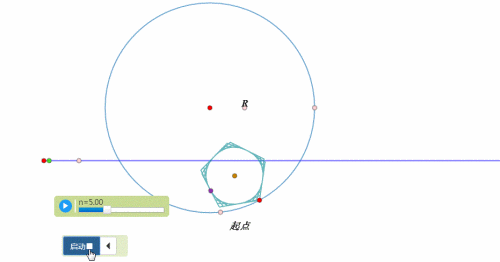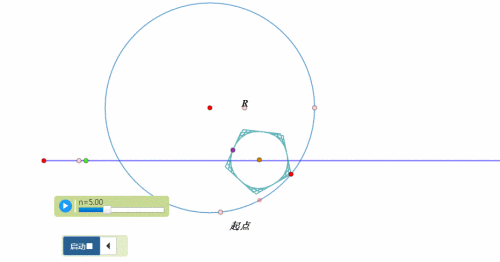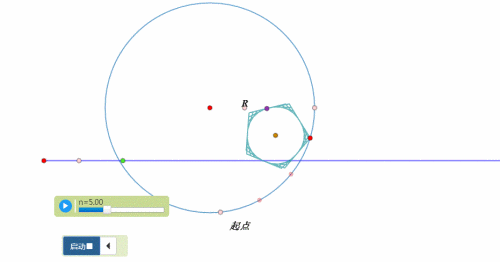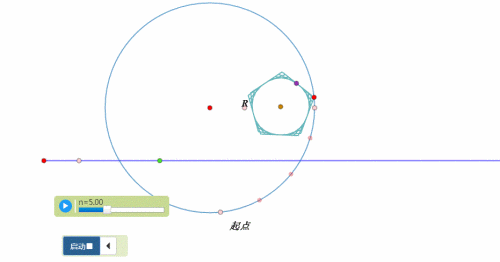
图形在圆上的滚动,分为两类:圆内、圆外。
例如,圆在圆外的滚动,正多边形在圆内滚动……

-
6
我们考虑更一般的情形:
给定某个图形,在另一条曲线上滚动,有没有办法实现统一模拟。
 END
END
注意事项
-
有两个想法,也就是能不能做两个工具:
-
合并曲线工具——选中若干条曲线,点击“合并曲线”工具,把这些被选中的曲线按先后顺序合并为一个整体。
-
滚动工具——依次选中两条曲线(先选中的要求是封闭曲线),可以轻松实现前者在后者上面的滚动。
-
这是我的想法,估计不可能实现。
经验内容仅供参考,如果您需解决具体问题(尤其法律、医学等领域),建议您详细咨询相关领域专业人士。
作者声明:本篇经验系本人依照真实经历原创,未经许可,谢绝转载。
展开阅读全部
文章评论