本文,用Mathematica来处理一则不等式的证明问题,并加以推广和拓展。

方法/步骤
-
1
题目是:
给定实数a和b,如果a+b=1,求证:
(a + 2)^2 + (b + 2)^2 >= 25/2

-
2
这里使用机器证明。

-
3
反过来考虑,当(a + 2)^2 + (b + 2)^2 <= 25/2时,a+b的值域是多少?
Mathematica给出的答案是,a+b最小值是-9,最大值是1。
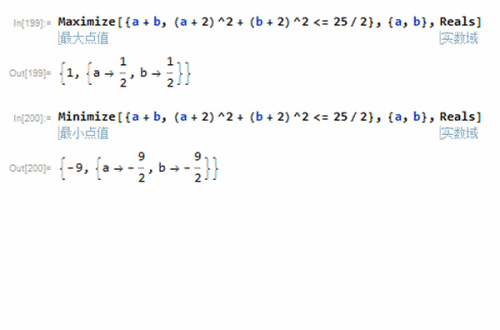
-
4
原问题可以加强为:
给定实数a和b,如果a+b>=1或者a+b<=-9,都有:
(a + 2)^2 + (b + 2)^2 >= 25/2

-
5
当(a + 2)^2 + (b + 2)^2 <= 25/2时,2a+3b的取值范围是:
[-(5/2)*(4 + Sqrt[26]),5*(-4 + Sqrt[26])/2]
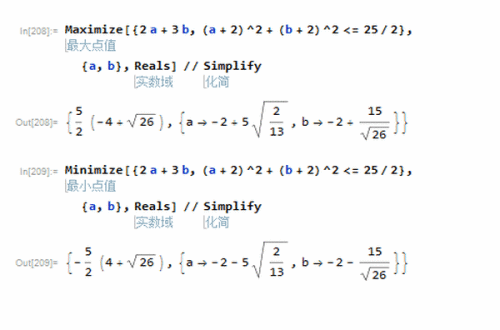
-
6
也就是说,当2a+3b的值在区间(-(5/2)*(4 + Sqrt[26]),5*(-4 + Sqrt[26])/2)之外的时候,
(a + 2)^2 + (b + 2)^2 >= 25/2恒成立。
 END
END
经验内容仅供参考,如果您需解决具体问题(尤其法律、医学等领域),建议您详细咨询相关领域专业人士。
作者声明:本篇经验系本人依照真实经历原创,未经许可,谢绝转载。
展开阅读全部
文章评论