怎样做立体几何题目

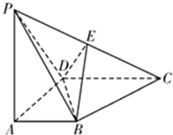
如图所示，四棱锥P-ABCD的底面是梯形，且BA1AD，CD丄AD，CD=2AB，PA 丄底面 ABCD，E 为 PC 的中点，PA=AD=AB=1．（1）证明：EB∥平面PAD；（2）求直线BD与平面PDC所成角的大小．

首先看第一问证明直线与平面平行，首先想到的当然是直线平行于平面内的一条直线。同时又有E为PC中点这一条件，看到中点就要想到作中位线！取取PD的中点Q，连接EQ、AQ，这样就得到了平行四边形ABEQ，故EB∥AQ，又AQ⊂平面PAD，EB⊄平面PAD故EB∥平面PAD

第一问就解决了

重点：①看到中点想到连接两个中点构成中位线②看到直线平行于平面就从直线平行于平面的一条直线着手

再来看第二问

求直线BD与平面PDC所成角的大小

求直线与平面所成角首先要做垂直，我们这里作垂直可以先大胆猜想BE就是垂直于平面PCD的，因为其他没有可以利用的条件了

有了这个猜想我们再来证明 第一问的条件和证明过程不是白用的

BE∥AQ，因此我们只需证明AQ⊥平面PCD

要证明AQ⊥平面PCD，我们只知道AQ⊥PD，因此还需证明AQ⊥CD

要证明AQ⊥CD，我们可以利用线面垂直，即CD⊥平面PAD

我们已经知道CD⊥AD，PA⊥CD，所以CD⊥平面PAD就证明完成了

再这样一步一步推回去就是证明过程了重点：①大胆假设 ②线线垂直想到线面垂直，线面垂直想到线线垂直 ③逆推

下面具体过程

（I）取PD的中点Q，连接EQ、AQ，则QE平行且等于1/2CD平行且等于AB

故四边形ABEQ是平行四边形．故EB∥AQ，又AQ⊂平面PAD，EB⊄平面PAD故EB∥平面PAD；（II）∵CD⊥AD，PA⊥CD，∴CD⊥平面PAD故AQ⊥CD，又可得AQ⊥PD，故AQ⊥平面PCD又BE∥AQ，故BE⊥平面PCD；所以∠BDE为所求角的平面角易得∠BDE=30°

考点解析

本题考点：

直线与平面平行的判定；直线与平面所成的角．

问题解析：

（I）欲证EB∥平面PAD，根据直线与平面平行的判定定理可知只需证EB与平面PAD内一直线平行，取PD的中点Q，连接EQ、AQ，易证四边形ABEQ是平行四边形则EB∥AQ，又AQ⊂平面PAD，EB⊄平面PAD，满足定理所需条件；（II）根据线面垂直的判定定理可知AQ⊥平面PCD，而BE∥AQ，则BE⊥平面PCD，从而∠BDE为所求角的平面角，在三角形BDE中求出此角即可．