MATALAB自定义函数的编写和调用方法

利用*.m函数定义函数

      这种方法需要定义一个*.m函数，包括输入参数，输出参数，函数体几个部分构成，调用函数时，直接调用函数名称即可。

   示例：已知平面两个点A,B的坐标分别为x1,y1,x2,y2，求A和B两点之间的距离，可以编写一个函数名称为dist.m(函数名称和M文件名称要一致),其具体内容为：

    function  distance = dist(x1, y1, x2, y2)

    distance = sqrt((x2-x1).^2 + (y2-y1).^2);

    具体调用时，直接调用dist(10,10,100,100)即可。

可用"type+函数文件名"查看函数的具体内容，或者用“help +函数文件名”

inline方式定义(可以直接定义而无需.m文件)。

    这种方式类似C++里的内联函数,运算速度较快，程序效率更高,但只能对数值进行代入。

    其格式为：f=inline('函数表达式','变量1','变量2',...) ；

 示例：求圆面积的函数，可以直接定义为：

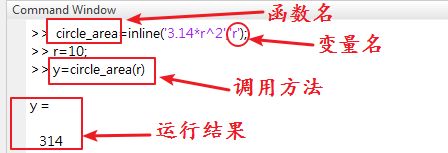
    circle_area=inline('3.14*r^2','r');  

    调用时，如果半径r=10，则直接用  y=circle_area(10)调用即可。 

syms+subs方式来进行调用(可以直接定义而无需.m文件)

用syms定义符号式，用subs来调用。

示例：求圆面积函数

       syms r  y;  

       y = 3.14*r^2;  

       subs(y,x,10) ;

匿名函数，直接通过@符号定义(可以直接定义和调用，无需.m文件)

    如图的示例，是求x和y的平方和z。

   还有下面一例：

power = @(x, n) x.^n;

result1 = power(7, 3)

result2 = power(49, 0.5)

程序运行后，可以得到以下结果：

>>

result1 =  343 

result2 =  7

主函数和子函数

      除了匿名函数以外的任何函数都必须在文件中定义。 

      主函数可以外部调用，用命令行的形式或者在函数中调用的形式。但子函数只能内部调用。子函数仅对于主函数或者相关的子函数中可见。

    示例：写一个名为“quadratic”的函数，来计算二次方程的根。 

   该函数的输入为：二次系数，线性系数和常数项(a,b,c)。 

   其输出为解得的二次方程的根(x1,x2)。

    其运行结果为：

>>quadratic(2,4,-4)%求解方程：a*x^2+b*x+c=0这个方程的根

ans = 0.7321 

嵌套函数

     在一个函数的主体中定义函数，被称为嵌套函数。 嵌套函数在其依附的另一个函数的范围内定义，与其一起共享工作空间的访问。

     示例：用嵌套函数实现求解一元二次方程。

（1）函数内容为：

function [x1,x2] = quadratic2(a,b,c)

function disc

  d = sqrt(b^2 - 4*a*c);

end   

disc;

x1 = (-b + d) / (2*a);

x2 = (-b - d) / (2*a);

end   

（2）其运行结果为：

>>quadratic2(2,4,-4)%求解方程：a*x^2+b*x+c=0这个方程的根

ans = 0.7321