本文用Thébault定理来证明如下的问题:
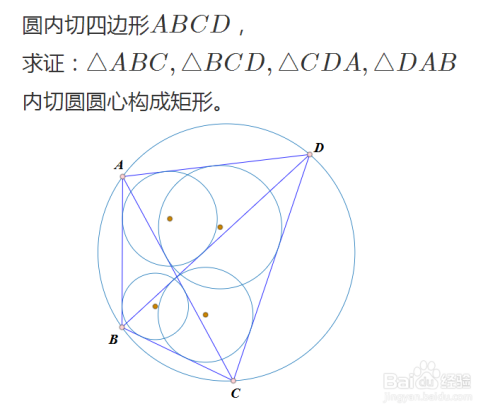
圆内接四边形ABCD,求证:△ABC、△BCD、△CDA、△DAB的内切圆圆心构成矩形。
方法/步骤
-
1
先介绍一下Thebault定理:
如下图,I、J、K三点共线,且KI:IJ=(tanu)^2。

-
2
下面开始处理原题。
先标记题目中四个三角形内切圆的圆心是Ia、Ib、Ic、Id。

-
3
假设对角线AC和BD交于X。
与线段AX、BX及外接圆相切的圆的圆心记为Ocd,
类似的,有Oda、Oab、Obc。

-
4
设AX与BX的夹角是2u,根据Thebault定理,可以证明:
Oda、Id、Ocd三点共线,且OcdId:IdOda=(tanu)^2。

-
5
同样的,Oab、Ia、Oda三点共线,且OabIa:IaOda=(tanu)^2。

-
6
所以,IaId//OabOcd。

-
7
原题结论成立。
 END
END
经验内容仅供参考,如果您需解决具体问题(尤其法律、医学等领域),建议您详细咨询相关领域专业人士。
作者声明:本篇经验系本人依照真实经历原创,未经许可,谢绝转载。
展开阅读全部
文章评论