本经验通过函数的定义域、单调性、凸凹性、极限等性质,介绍函数用导数工具画函数y=ln(-5x/8)的图像的主要步骤。
主要方法与步骤
-
1
函数为自然对数函数,自变量可以取负数,即定义域为:(-∞,0)。
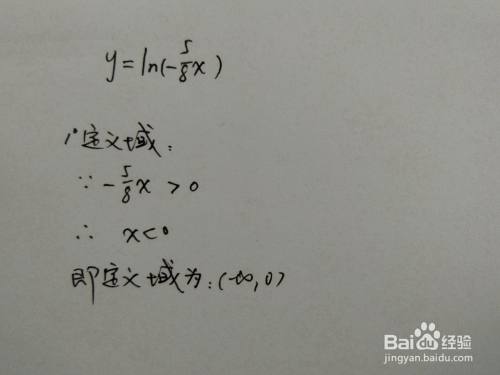
-
2
函数的单调性,通过函数的一阶导数,判断函数的单调性。

-
3
函数的凸凹性,通过函数的二阶导数,解析函数的凸凹性。

-
4
函数的极限,函数在端点处的极限。设函数f(x)在x0处的某一去心邻域内有定义,若存在常数A,对于任意ε>0,总存在正数δ,使得当|x-xo|<δ时,|f(x)-A|<ε成立,那么称A是函数f(x)在x0处的极限。

-
5
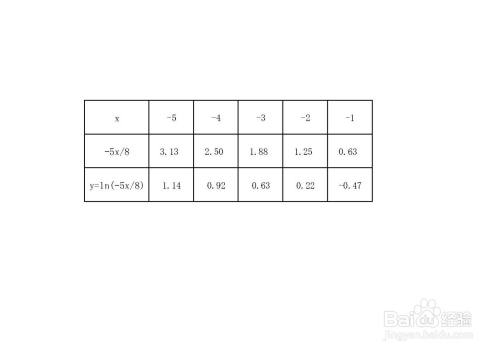
函数上部分点列表,以五点图表显示如下图所示。
-
6
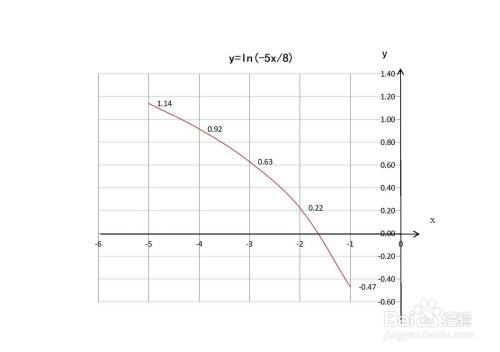
函数的示意图,综合以上函数的性质,函数的示意图如下:
 END
END
经验内容仅供参考,如果您需解决具体问题(尤其法律、医学等领域),建议您详细咨询相关领域专业人士。
作者声明:本篇经验系本人依照真实经历原创,未经许可,谢绝转载。
展开阅读全部
文章评论