MATLAB符号运算求一元二次方程的根

第一，要求解的一元二次方程如下图，共三个。

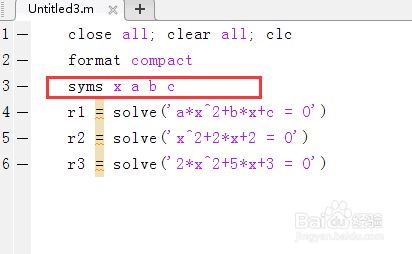
第二，启动MATLAB，先利用第一方法syms定义符号变量，输入以下代码，求上述三个一元二次方程的根。

close all; clear all; clc

format compact

syms x a b c

r1 = solve('a*x^2+b*x+c = 0')

r2 = solve('x^2+2*x+2 = 0')

r3 = solve('2*x^2+5*x+3 = 0')

第三，保存和运算上述代码，得到上述三个一元二次方程的根如下：

r1 =

 -(b + (b^2 - 4*a*c)^(1/2))/(2*a)

 -(b - (b^2 - 4*a*c)^(1/2))/(2*a)

r2 =

 - 1 + i

 - 1 - i

r3 =

   -1

 -3/2

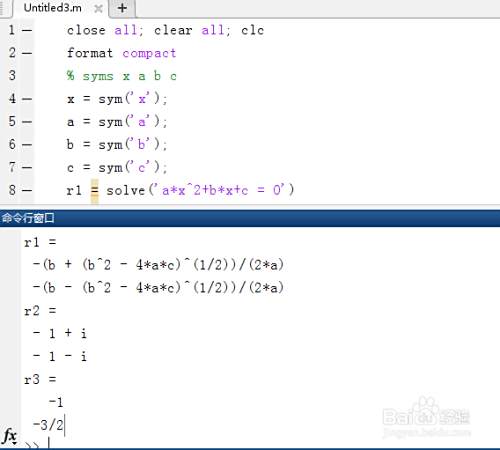
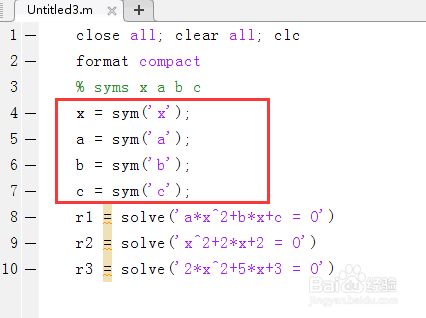
第四，再利用第二方法sym(' ')定义符号变量，输入以下代码，求上述三个一元二次方程的根。

close all; clear all; clc

format compact

% syms x a b c

x = sym('x');

a = sym('a');

b = sym('b');

c = sym('c');

r1 = solve('a*x^2+b*x+c = 0')

r2 = solve('x^2+2*x+2 = 0')

r3 = solve('2*x^2+5*x+3 = 0')

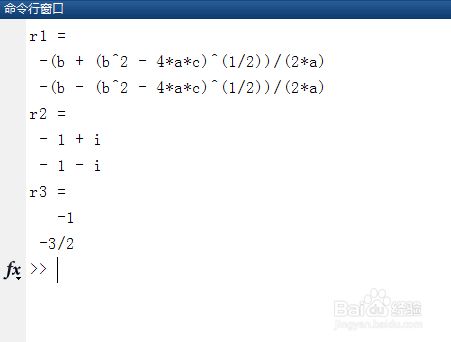
第五，保存和运行上述代码，得到的结果与第三步相同。

r1 =

 -(b + (b^2 - 4*a*c)^(1/2))/(2*a)

 -(b - (b^2 - 4*a*c)^(1/2))/(2*a)

r2 =

 - 1 + i

 - 1 - i

r3 =

   -1

 -3/2

第六，syms方法与sym(' ')方法相比，第一种方法定义符号变量更简介，可以一次定义多个符号变量。