在三角形里面,它的重心、垂心、外心共线,这条线就是三角形的欧拉线。
下面就用画板来验证一下,这三个点共线的原因。

方法/步骤
-
1
设A是线段BC上的动点,测量A在线段BC上的相对值m000,其实就是BA与BC的长度之比。
-
2
绘制△DEF的垂心H和重心G,同时保留三条高。
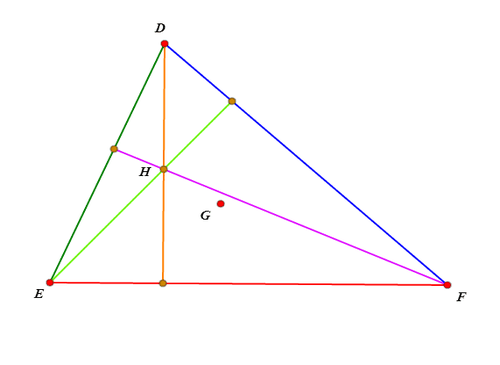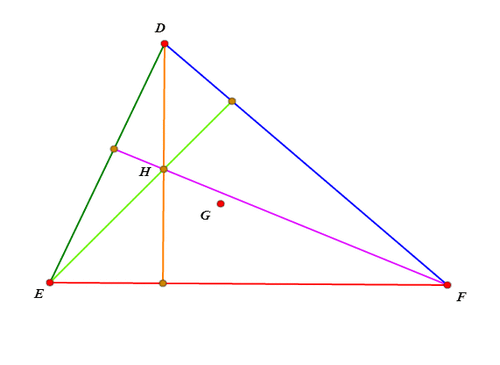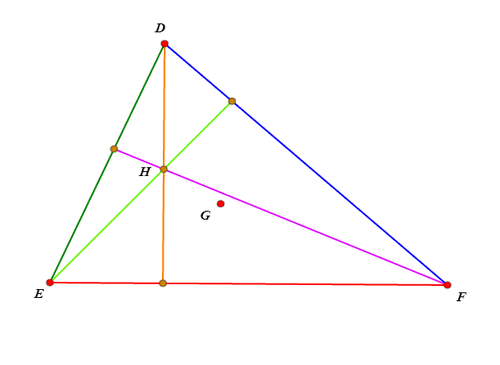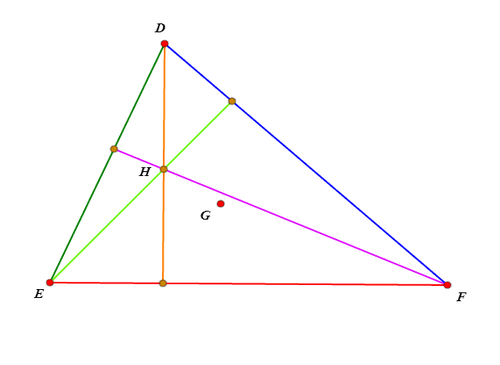
-
3
选择△DEF内所有的几何图形,再双击点G,进行逆时针的旋转变换,旋转弧度是pi*m000,得到的图形是:△D'E'F'和垂心H',还有三条高。

-
4
选择△D'E'F'和垂心H',还有三条高,最后选择点G,进行缩放变换,缩放比是1-m000/2,得到的图形是:△D''E''F''和垂心H'',还有三条高。
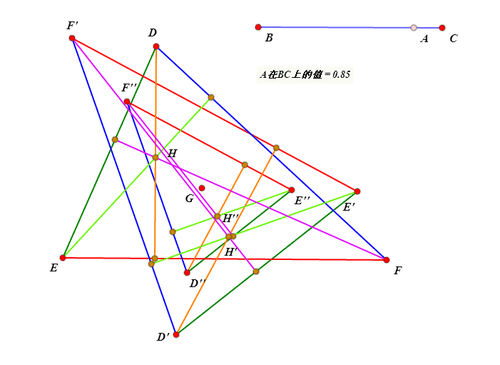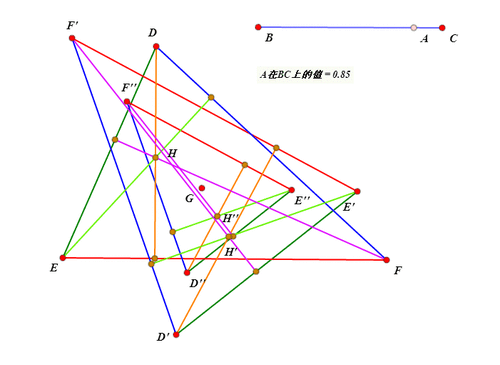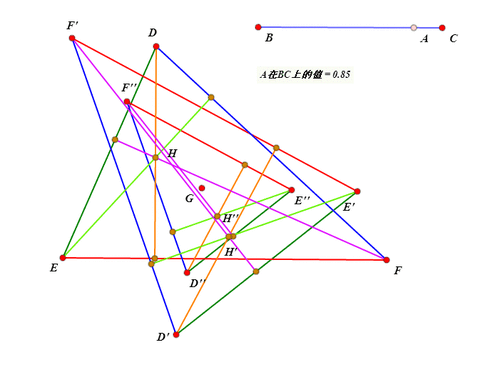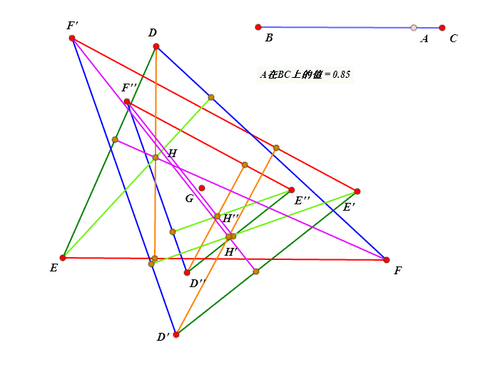
-
5
隐藏选择△D'E'F'和垂心H',还有三条高,使图形显得比较清楚。

-
6
构造点A的动画。
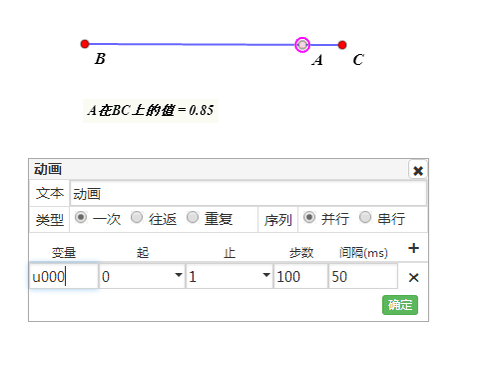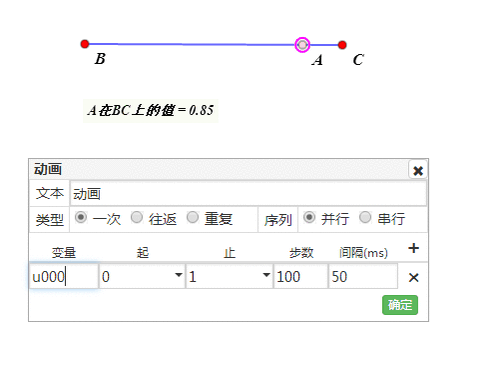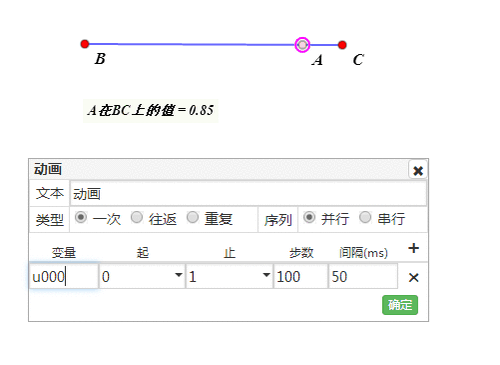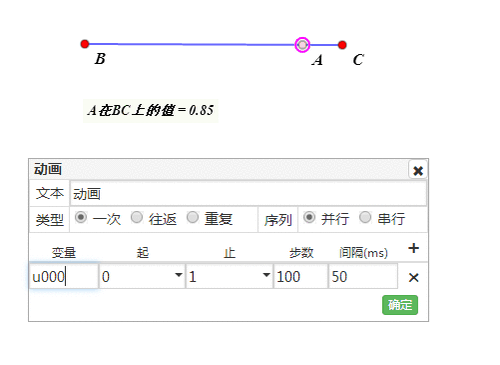
-
7
播放动画,可以发现,当A与C重合的时候,H''恰好就是△DEF的外心。
 END
END
经验内容仅供参考,如果您需解决具体问题(尤其法律、医学等领域),建议您详细咨询相关领域专业人士。
作者声明:本篇经验系本人依照真实经历原创,未经许可,谢绝转载。
展开阅读全部
文章评论